Математическая статистика
![]() Регрессионный анализ
Регрессионный анализ
Задачи регрессионного анализа
Рассмотрим задачу определения значения случайной величины по данным значениям другой величины. Пусть Y – случайная величина, значения которой требуется определить, x – известная величина, которая может представлять собой значение некоторой случайной величины X или заданное значение некоторой переменной. Предположим, что между величинами Y и X имеется статистическая связь, т.е. распределение случайной величины Y зависит от значения x.
С точки зрения математической статистики поставленная задача представляет собой задачу оценивания значения случайной величины Y при данном значении x. Пусть $\hat{y}=\hat{y}(x)$ – оценка значения случайной величины Y при данном значении x. В связи с тем, что x – фиксированное значение, то оценка $\hat{y}$ не является случайной величиной. Случайной величиной является ошибка этой оценки:
|
$\varepsilon (x)=\hat{y}(x)-Y$. |
В качестве меры точности оценки $\hat{y}(x)$ целесообразно использовать математическое ожидание квадрата ошибки $\varepsilon (x)$:
|
${{m}_{{{\varepsilon }^{2}}}}(x)=\text{M}\left[ {{\left( \hat{y}(x)-Y \right)}^{2}}|x \right]$. |
Наилучшей оценкой значения случайной величины Y при данном значении x будет оценка, минимизирующая ошибку (2):
|
$\text{M}\left[ {{\left( \hat{y}(x)-Y \right)}^{2}}|x \right]\to \underset{\hat{y}(x)}{\mathop{\min }}\,$. |
Из известного в теории вероятностей равенства
|
$\text{M}\left[ {{\left( Y-a \right)}^{2}} \right]=\text{D}[Y]+{{\left( \text{M}[Y]-a \right)}^{2}}$ |
следует, что математическое ожидание квадрата ошибки (1) будет минимальным, если $\hat{y}(x)$ будет математическим ожиданием случайной величины Y при данном значении x:
|
$\hat{y}(x)=\text{M}\left[ Y|x \right]$. |
Следовательно, зависимость оценки $\hat{y}(x)$ значения случайной величины Y при данном значении x представляет собой регрессию Y на X. Таким образом, оптимальной с точки зрения среднего квадрата ошибки (1) оценкой зависимости Y от x служит регрессия Y на X. В частности, оптимальным прогнозом величины Y по данному значению x будет прогноз по регрессии.
Модель, определяемая регрессией Y на X, называется регрессионной моделью. Построение и исследование регрессионных моделей составляет предмет регрессионного анализа.
Регрессионную модель имеет смысл строить, если априорно или по результатам предварительного анализа выявлено, что между входными и выходными величинами имеется статистическая связь. В терминах регрессионного анализа входные величины называются регрессорами, или предикторами, а выходные переменные - откликами модели.
Ниже перечислены основные задачи регрессионного анализа.
1) Выбор класса функций для описания зависимости откликов модели ${{Y}_{1}},...,{{Y}_{l}}$ от регрессоров ${{X}_{1}},...,{{X}_{m}}$.
2) Нахождение оценок неизвестных параметров функции, описывающей зависимость откликов модели ${{Y}_{1}},...,{{Y}_{l}}$ от регрессоров ${{X}_{1}},...,{{X}_{m}}$.
3) Статистический анализ найденной зависимости откликов модели ${{Y}_{1}},...,{{Y}_{l}}$ от регрессоров ${{X}_{1}},...,{{X}_{m}}$.
4) Предсказание значений откликов модели ${{Y}_{1}},...,{{Y}_{l}}$ по результатам наблюдения регрессоров ${{X}_{1}},...,{{X}_{m}}$ на основе найденной зависимости.
Рассмотрим случай одного регрессора X и скалярного отклика Y.
Как показано выше, оптимальной функцией, описывающей зависимость отклика модели Y от регрессора X, является функция регрессии Y на X. При этом возможны следующие ситуации.
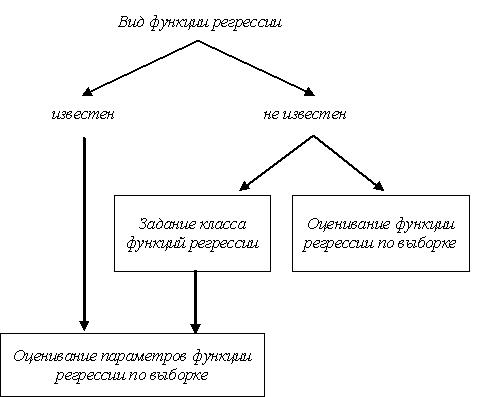
1) Вид функции регрессии известен, исходя из априорной информации о наблюдаемых величинах. Например, если известно, что случайные величины X и Y имеют нормальный закон распределения, то уравнение регрессии Y на X (как и X на Y) может быть только линейным.
2) Вид функции регрессии не известен или эта функция слишком сложна. В этой ситуации возможны следующие подходы к определению вида функции регрессии.
а) Исследователь задаёт некоторый ограниченный класс функций Ψ, например, линейные или полиномиальные функции, в котором предлагается искать функцию регрессии. Если этот класс функций не содержит «истинную» функцию регрессии, то минимум среднего квадрата ошибки $\varepsilon (x)$ при каждом значении x не может быть обеспечен. На практике ищут оценку зависимости $\hat y(x)$ в выбранном классе функций из условия минимума математического ожидания (2) квадрата ошибки $\varepsilon (x)$ в рассматриваемой области изменения величины x. Для выбора класса функций, в котором целесообразно искать функцию регрессии, нередко требуется проведение предварительного анализа результатов наблюдений.
б) Функция регрессии оценивается по результатам наблюдений. Такое оценивание основано на расчёте множества условных средних значений наблюдений отклика Y и аппроксимации линии регрессии по рассчитанным точкам.
|
|
|









