Математическая статистика
![]() Анализ статистических взаимосвязей
Анализ статистических взаимосвязей
Оценивание коэффициента детерминации и корреляционного отношения по выборочным данным
Пусть (x1, y1),…, (xn, yn) – выборка наблюдений двумерного случайного вектора (X, Y), имеющего неизвестное распределение FXY(x, y).
1. Точечные оценки КД и КО
В качестве точечной оценки коэффициента детерминации используют статистику
|
$R_{Y|X}^{2*}=\frac{D_{Y|X}^{*}}{D_{Y}^{*}}=1-\frac{D_{resY}^{*}}{D_{Y}^{*}}$. |
Такую оценку КД называют также показателем «эр-квадрат» (R-squared).
В качестве точечной оценки корреляционного отношения используют статистику
$R_{Y|X}^{*}=\sqrt{\frac{D_{Y|X}^{*}}{D_{Y}^{*}}}=\sqrt{1-\frac{D_{resY}^{*}}{D_{Y}^{*}}}$.
Для расчёта выборочной остаточной дисперсии $D_{resY}^{*}$ необходимо знать функцию регрессии Y на X. Пусть эта функция имеет вид $f({{x}_{i}},{{\beta }_{0}},...,{{\beta }_{k-1}})$, где ${{\beta }_{0}},...,{{\beta }_{k-1}}$ – известные параметры. Тогда, учитывая определение остаточной дисперсии, запишем выражение для выборочной остаточной дисперсии:
|
$D_{resY}^{*}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{\left( {{y}_{i}}-f({{x}_{i}},{{\beta }_{0}},...,{{\beta }_{k-1}}) \right)}^{2}}}$. |
Если же для функции регрессии задан только её вид, а параметры ${{\beta }_{0}},...,{{\beta }_{k-1}}$ оцениваются на основе результатов наблюдений (x1,y1),…,(xn,yn), то выборочная остаточная дисперсия рассчитывается по формуле
$D_{resY}^{*}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{\left( {{y}_{i}}-f({{x}_{i}},{\tilde{\beta}_0},...,{\tilde{\beta}_{k-1}}) \right)}^2}}$,
где ${{\tilde{\beta }}_{0}},...,{{\tilde{\beta }}_{k-1}}$ – оценки параметров ${{\beta }_{0}},...,{{\beta }_{k-1}}$.
Выборочная дисперсия признака Y рассчитывается по известной формуле:
$D_{Y}^{*}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{\left( {{y}_{i}}-\bar{y} \right)}^{2}}}$.
При обработке реальных данных встречаются случаи, когда ни вид, ни параметры функции регрессии бывают априорно не известны. В этом случае функция регрессии может быть оценена непосредственно по выборочным наблюдениям. Для этого проводится группировка выборочных значений x1,…,xn. Обозначим J1,…,Jk – интервалы группировки, ni – число выборочных точек, попадающих в интервал Ji, $i=\overline{1,k}$, k – число интервалов.
Пусть $({{x}_{i1}},{{y}_{i1}}),...,({{x}_{i,{{n}_{i}}}},{{y}_{i,{{n}_{i}}}})$ – выборочные наблюдения, попавшие в интервал Ji, $i=\overline{1,k}$. Для этих наблюдений рассчитываются групповые средние $({{\bar{x}}_{i}},{{\bar{y}}_{i}})$, где
${{\bar{x}}_{i}}=\frac{1}{{{n}_{i}}}\sum\limits_{j=1}^{{{n}_{i}}}{{{x}_{ij}}},\ \ \ \ {{\bar{y}}_{i}}=\frac{1}{{{n}_{i}}}\sum\limits_{j=1}^{{{n}_{i}}}{{{y}_{ij}}}.$
Линия, соединяющая все групповые средние $({{\bar{x}}_{1}},{{\bar{y}}_{1}}),...,({{\bar{x}}_{m}},{{\bar{y}}_{m}})$, и будет являться оценкой линии регрессии.
На практике для упрощения вычислений при расчёте оценки дисперсии, обусловленной регрессией Y на X, предполагается, что функция регрессии является кусочно-постоянной:
$\forall x\in {{J}_{i}}\to f(x)={{\bar{y}}_{i}},\ i=\overline{1,k}$.
Число интервалов группировки k не должно быть слишком мало – в этом случае кусочно-постоянная аппроксимация функции регрессии будет неточной. С другой стороны, при слишком большом числе интервалов группировки становятся неточными оценки групповых средних.
Учитывая определение дисперсии, обусловленной регрессией, запишем выражение для выборочной дисперсии, обусловленной регрессией Y на X:
|
$D_{Y|X}^{*}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{n}_{i}}{{\left( {\bar{y}_{i}}-\bar{y} \right)}^{2}}}$. |
Можно показать, что для выборочных оценок общей дисперсии Y, дисперсии, обусловленной регрессией Y на X, и остаточной дисперсии Y справедливо правило сложения дисперсий:
$D_{Y}^{*}=D_{resY}^{*}+D_{Y|X}^{*}$.
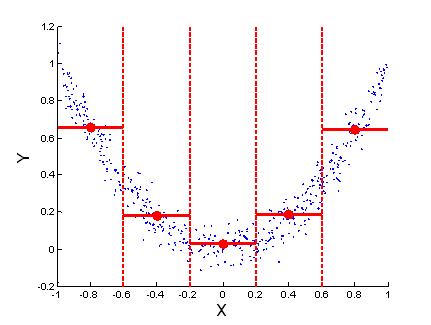
Оценивание линии регрессии по выборочным данным. Жирными точками отмечены групповые средние $({{\bar{x}}_{1}},{{\bar{y}}_{1}}),...,({{\bar{x}}_{m}},{{\bar{y}}_{m}})$
При расчётах дисперсии, обусловленной регрессией, остаточной дисперсии и общей дисперсии, а также КД и КО по результатам выборочного наблюдения необходимо иметь в виду, что все получаемые значения являются смещёнными оценками соответствующих теоретических значений, характеризующих генеральную совокупность. Показатели вариации, а также их несмещённые оценки сведены в таблицу, называемую таблицей регрессионного анализа (табл. 6.5).
Таблица 6.5
Таблица регрессионного анализа
Источник вариации |
Показатель вариации |
Число степеней свободы |
Несмещённая оценка |
Регрессия |
$D_{Y|X}^{*}$ |
k–1 |
$\frac{n}{k-1}D_{Y|X}^{*}$ |
Остаточные признаки |
$D_{resY}^{*}$ |
n–k |
$\frac{n}{n-k}D_{resY}^{*}$ |
Все признаки |
${{D}_{Y}^*}$ |
n–1 |
$\frac{n}{n-1}{{D}_{Y}^*}$ |
Здесь k – число оцениваемых параметров функции регрессии. Если при расчётах используется кусочно-постоянная аппроксимация функции регрессии, то это число равно числу интервалов группировки.
Смещение точечной оценки КД, рассчитываемой по формуле (1), равно
$\text{M}\left[ R_{Y|X}^{2*} \right]-R_{Y|X}^{2}=\frac{1-R_{Y|X}^{2}}{n}\left( k-(1-R_{Y|X}^{2})(1+2R_{Y|X}^{2}) \right)$.
Это смещение всегда положительно, т.е. оценка КД (1) в среднем даёт завышенную долю дисперсии, объясненной регрессией. При больших k и малых n это смещение может достигать существенных значений и приводить к серьёзным ошибкам в интерпретации получаемых результатов. В частности, при $R_{Y|X}^{2}=0$ смещение оценки КД равно
$\text{M}\left[ R_{Y|X}^{2*}|R_{Y|X}^{2}=0 \right]=\frac{k-1}{n}$.
Пренебрегая единицей в числителе, это смещение имеет смысл величины, обратной числу наблюдений, приходящихся на один оцениваемый параметр уравнения регрессии. Например, для выборки объёма n = 18 из генеральной совокупности с КД, равным нулю, при числе оцениваемых параметров уравнения регрессии k = 6 (таким образом, три наблюдения на параметр), оценка КД в среднем будет равна 5/18 = 0,278. При $n/k>100$ смещение выборочного значения КД становится менее 0,01.
Оценкой КД, имеющей меньшее смещение, является отношение несмещённых оценок остаточной дисперсии и общей дисперсии признака Y за вычетом из единицы:
|
$\bar{R}_{Y|X}^{2}=1-\frac{\tilde{D}_{resY}}{\tilde{D}_{Y}}$, |
где
$\tilde{D}_{resY}^{{}}=\frac{n}{n-k}D_{resY}^{*}$,
$\tilde{D}_{Y}^{{}}=\frac{n}{n-1}D_{Y}^{*}$.
Учитывая выражение для расчёта показателя $R_{Y|X}^{2*}$, запишем:
|
$\bar{R}_{Y|X}^{2}=1-\frac{{D_{resY}^{*}}/{(n-k)}\;}{{D_{Y}^{*}}/{(n-1)}\;}=1-\left( 1-R_{Y|X}^{2*} \right)\frac{n-1}{n-k}$. |
Эта оценка по-прежнему является смещённой, поскольку отношение двух несмещённых оценок в общем случае не является несмещённой оценкой отношения. Такая оценка называется скорректированной оценкой коэффициента детерминации. Скорректированную оценку КД называют также показателем «эр-бар-квадрат» (adjusted R-squared).
Показатели «эр-квадрат» и «эр-бар-квадрат» имеют принципиально различную интерпретацию. Показатель $R_{Y|X}^{2*}$ является мерой вариации признака Y, объяснённой регрессией f(x). Если вариация выборочных данных относительно линии регрессии отсутствует, т.е. все выборочные наблюдения лежат на линии регрессии, то $R_{Y|X}^{2*}=1$. Если вариация самой линии регрессии отсутствует, т.е. $f(x)=const$, то $R_{Y|X}^{2*}=0$.
Показатель $\bar{R}_{Y|X}^{2}$ всегда меньше показателя $R_{Y|X}^{2*}$ и может даже принимать отрицательные значения. Этот показатель можно рассматривать как сравнительную меру «объяснительных» способностей различных уравнений регрессии.
При большом отношении $n/k$ объёма выборки к числу параметров уравнения регрессии разница между $R_{Y|X}^{2*}$ и $\bar{R}_{Y|X}^{2}$ становится практически пренебрежимой.
2. Интервальные оценки КД и КО
При расчёте границ доверительных интервалов для КД и КО используются различные аппроксимации. Если распределение FXY(x, y) является двумерным нормальным распределением, то доверительный интервал на уровне значимости a для КД $R_{Y|X}^{2}$ может быть аппроксимирован следующим интервалом:
$\left( R_{Y|X}^{2*}-{{t}_{1-\alpha /2}}(n-k-1)s\left[ R_{Y|X}^{2*} \right];R_{Y|X}^{2*}+{{t}_{1-\alpha /2}}(n-k-1)s\left[ R_{Y|X}^{2*}\right] \right)$,
где ${{t}_{1-\alpha /2}}(n-k-1)$ – квантиль распределения Стьюдента с n–k–1 степенями свободы на уровне 1–α/2, а $s\left[ R_{Y|X}^{2*} \right]$ – оценка с.к.о. показателя «эр-квадрат», рассчитываемая из формулы:
${{s}^{2}}\left[ R_{Y|X}^{2*} \right]=\frac{4R_{Y|X}^{2*}{{\left( 1-R_{Y|X}^{2*} \right)}^{2}}{{\left( n-k \right)}^{2}}}{\left( {{n}^{2}}-1\right)\left( n+3 \right)}$,
которая при $n >> k$ может быть аппроксимирована выражением:
${{s}^{2}}\left[ R_{Y|X}^{2*} \right] \approx \frac{4R_{Y|X}^{2*}{{\left( 1-R_{Y|X}^{2*} \right)}^{2}}}{n}$,
Для расчёта доверительного интервала для КО $R_{Y|X}^{{}}$ используется аппроксимация:
$\left( \sqrt{\frac{(n-k)R_{Y|X}^{2*}}{n\left( 1-R_{Y|X}^{2*} \right){{f}_{1-\alpha/2}}({{r}_{1}},{{r}_{2}})}-\frac{k-1}{n}};\sqrt{\frac{(n-k)R_{Y|X}^{2*}}{n\left( 1-R_{Y|X}^{2*} \right){{f}_{\alpha/2}}({{r}_{1}},{{r}_{2}})}-\frac{k-1}{n}} \right)$,
где ${{f}_{\alpha /2}}({{r}_{1}},{{r}_{2}})$ и ${{f}_{1-\alpha /2}}({{r}_{1}},{{r}_{2}})$ – квантили распределения Фишера с r1 и r2 степенями свободы в числителе и в знаменателе на уровнях α/2 и 1–α/2 соответственно. Степени свободы вычисляются по формулам:
${{r}_{1}}=\left[ \frac{{{\left( k-1+nR_{Y|X}^{2*} \right)}^{2}}}{k-1+2nR_{Y|X}^{2*}} \right],$
${{r}_{2}}=n-k,$
где $[\cdot ]$ – целая часть числа.
На практике указанные аппроксимации применяются и для случая, когда распределение FXY(x, y) отличается от нормального, причём, чем больше отношение $n/k$, тем выше точность аппроксимации.
3. Проверка значимости КД и КО
Для проверки статистической гипотезы
${{H}_{0}}:R_{Y|X}^{2}=0$ (или ${{H}_{0}}:R_{Y|X}^{{}}=0$)
в качестве статистики критерия используют статистику
|
$Z=\frac{{R_{Y|X}^{2*}}/{(k-1)}\;}{{\left( 1-R_{Y|X}^{2*} \right)}/{(n-k)}\;}$, |
которая при условии истинности H0 имеет распределение Фишера с k–1 и n–k степенями свободы в числителе и в знаменателе соответственно: ${{f}_{Z}}(z|{{H}_{0}})\sim F(k-1,n-k)$.
Критическая область для статистики критерия выбирается правосторонней.
|
|
|









