Математическая статистика

Как только определён класс функций Ψ, в котором предлагается искать функцию регрессии, возникает задача оценивания её параметров. Рассмотрим сначала случай одного регрессора X и скалярного отклика Y. Пусть $f(x,{{\beta }_{0}},...,{{\beta }_{k-1}})\in \Psi $ – предполагаемая скалярная функция регрессии, $\beta ={{({{\beta }_{0}},...,{{\beta }_{k-1}})}^{T}}$ – вектор неизвестных параметров.

Таким образом, принимая во внимание (1*) и (5*), случайная величина Y при фиксированном значении x представляет собой сумму двух слагаемых: неслучайной величины $f(x,{{\beta }_{0}},...,{{\beta }_{k-1}})$ и случайной ошибки $\varepsilon (x)$:

Модель (1) является регрессионной моделью отклика Y, а ошибка $\varepsilon (x)$ называется ошибкой регрессионной модели.

При оценивании и проведении статистического анализа регрессионной модели (1), как правило, выдвигаются следующие ключевые требования.

1°. Математическое ожидание ошибки модели $\varepsilon (x)$ для всех x из рассматриваемой области изменения равно нулю:

$\text{M}\left[ \varepsilon (x) \right]=0$.

Если математическое ожидание $\text{M}\left[ \varepsilon (x) \right]=const\neq 0$, то это требование может быть обеспечено для любых предполагаемых функций регрессии со свободным членом, поскольку он берёт на себя возможное ненулевое математическое ожидание ошибок. В связи с этим выбор моделей со свободным членом, как правило, предпочтительнее.

Нарушение этого требования в общем случае приводит к смещённости оценок регрессионной модели.

2°. Вход модели X и ошибки модели $\varepsilon (x)$ для всех x из рассматриваемой области изменения – независимые случайные величины. Это требование называется требованием экзогенности входа модели.

Экзогенность входа X означает независимость случайной величины X от функционирования моделируемой системы. Значения экзогенных переменных определяются вне модели и не связаны с результатами работы системы.

Примером неэкзогенной модели является модель:

${{Y}_{t}}=f({{Y}_{t-1}},{{\beta }_{0}},...,{{\beta }_{k-1}})+{{\varepsilon }_{t}}$.

В этой модели вход ${{Y}_{t-1}}$, очевидно, зависит от ошибки модели ${{\varepsilon }_{t-1}}$.

Нарушение требования экзогенности приводит к существенному ухудшению статистических свойств оценок регрессионной модели.

Пусть (x₁, y₁),…,(x_n, y_n) – выборка наблюдений двумерного случайного вектора (X, Y), имеющего распределение F_XY(x, y).

Оптимальным вектором параметров β будет вектор, при котором достигается минимум критерия (3*) при каждом x. В силу ограниченности объёма выборки в качестве меры точности регрессионной модели выберем оценку среднего квадрата ошибки при каждом выборочном значении ${{x}_{1}},...,{{x}_{n}}$:

которая в точности совпадает с выражением (2*) для остаточной дисперсии признака Y.

Таким образом, задача нахождения вектора параметров β – это задача минимизации критерия:

Учитывая, что выборочная дисперсия $D_{Y}^{*}$ случайной величины Y не зависит от β, критерий минимизации остаточной дисперсии (3) эквивалентен критерию максимизации показателя «эр-квадрат»:

Вектор $\tilde{\beta }$, максимизирующий критерий (4), является точечной оценкой вектора параметров β функции регрессии$f(x,\beta )\in \Psi $, рассчитанной по выборке (x₁, y₁),…,(x_n, y_n). Метод расчёта вектора $\tilde{\beta }$, основанный на минимизации критерия (4), называется методом наименьших квадратов (МНК), а рассчитанные с его помощью оценки ${{\tilde{\beta }}_{0}},...,{{\tilde{\beta}}_{k-1}}$ называются МНК-оценками.

Поскольку показатель «эр-квадрат», минимизируемый в методе наименьших квадратов, характеризует долю вариации случайной величины Y, объяснённую функцией регрессии, суть метода наименьших квадратов состоит в подборе таких параметров функции регрессии из заданного класса функций Ψ, при которых она объясняет максимально возможную долю вариации признака Y.

Необходимым условием минимума функции $D_{resY}^{*}(\beta )$ является равенство нулю частных производных:

Подставляя (2) в выражение (5), получим систему k уравнений с k неизвестными:

Разрешая эту систему относительно параметров ${{\beta }_{0}},...,{{\beta }_{k-1}}$, находим МНК-оценки ${{\tilde{\beta }}_{0}},...,{{\tilde{\beta}}_{k-1}}$ параметров функции регрессии $f(x,{{\beta }_{0}},...,{{\beta }_{k-1}})$. Значение $\tilde{f}(x)=f(x,{{\tilde{\beta}}_{0}},...,{{\tilde{\beta }}_{k-1}})$ представляет собой МНК-оценку функции регрессии в точке x.

Таким образом, оценка регрессионной модели (1) имеет вид:

Подставляя выборочные значения ${{x}_{1}},...,{{x}_{n}}$ в модель (7), получим множество случайных величин ${{\tilde{Y}}_{1}},...,{{\tilde{Y}}_{n}}$, предсказанных моделью:

${{\tilde{Y}}_{i}}=\tilde{f}({{x}_{i}})+\varepsilon ({{x}_{i}})$.

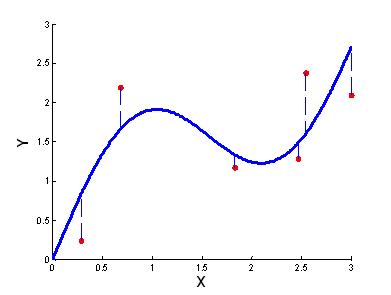
Реализациями случайных величин ${{\tilde{Y}}_{1}},...,{{\tilde{Y}}_{n}}$ являются выборочные значения ${{y}_{1}},...,{{y}_{n}}$. Разности между наблюдаемыми значениями ${{y}_{1}},...,{{y}_{n}}$ и расчётными значениями функции регрессии $\tilde{f}({{x}_{1}}),...,\tilde{f}({{x}_{n}})$, называются регрессионными остатками (residuals):

$\tilde{\varepsilon }({{x}_{i}})={{y}_{i}}-\tilde{f}({{x}_{i}})$, $i=\overline{1,n}$.

Регрессионные остатки $\tilde\varepsilon(x_1),...,\tilde\varepsilon(x_n)$ являются реализациями случайных ошибок $\varepsilon(x_1),...,\varepsilon(x_n)$ регрессионной модели (1) при значениях её входа, равных ${{x}_{1}},...,{{x}_{n}}$ соответственно.

Можно показать, что при соблюдении требований 1° и 2° к регрессионной модели, оценки параметров ${{\tilde{\beta }}_{0}},...,{{\tilde{\beta}}_{k-1}}$ функции регрессии и её значения $\tilde{f}(x)$ в произвольной точке x являются состоятельными и несмещёнными.