Математическая статистика
![]() Регрессионный анализ
Регрессионный анализ
Статистические модели
Для применения математических методов описания явлений необходимо, прежде всего, установить соотношения между величинами, характеризующими рассматриваемые явления. Каждое такое соотношение представляет собой математическую модель явления. Так, например, законы Ньютона представляют собой совокупность моделей механических явлений. Уравнения Максвелла в физике представляют собой математическую модель электродинамических явлений.
Пусть поведение системы описывается некоторой совокупностью величин, причём одни величины носят характер внешних воздействий на систему и называются её входными воздействиями (input variables), а другие представляют собой результат работы системы и называются откликами системы (responses) на входные воздействия.
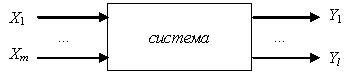
Во многих случаях математическую модель системы можно построить чисто математическим путём на основе известных законов механики, физики и других дисциплин, использующих количественные соотношения (такую модель будем называть теоретической). Так, например, различные модели управляемого летательного аппарата можно построить математически, пользуясь законами механики.
Однако существуют и такие системы, для которых принципиально невозможно построить модели чисто математическим путём. Примерами таких систем могут служить человек или коллектив людей, завод, отрасль промышленности, экономика и т.п. В этом случае приходится прибегать к экспериментальному исследованию самих систем или входящих в них подсистем и строить соответствующие модели путём статистической обработки полученных данных.
Модели, построенные на основе статистической обработки результатов экспериментального исследования функционирования систем, называются статистическими моделями систем.
Примерами задач, при решении которых используются статистические модели, могут служить прогнозирование погоды по измеренным значениями параметров состояния атмосферы в различных точках пространства и в различные моменты времени, в медицинской практике задача распознавания болезни пациента по результатам обследования и определение соответствующих методов лечения, распознавание рукописных символов и цифр на изображении и многие другие задачи, для решения которых применение классических математических методов оказывается неэффективным.
Задача построения статистической модели явления, процесса или системы состоит в нахождении соотношений между величинами, описывающими течение данного явления, процесса или функционирование системы. Если эти соотношения позволяют по данным значениям входных величин однозначно определить значения выходных, то описываемая ими модель называется детерминированной. Если же выходы модели являются случайными величинами, то модель называется стохастической.
Как теоретические модели, выводимые математически из законов физики, химии, экономики или других областей науки, так и статистические модели, получаемые на основе статистической обработки результатов наблюдений, могут быть детерминированными или стохастическими.
Одному и тому же явлению могут соответствовать различные модели. Проблема построения модели системы включает выбор подходящей формы этой модели, а также разумной степени её сложности.
|
|









