Математическая статистика
![]() Анализ статистических взаимосвязей
Анализ статистических взаимосвязей
Статистическая связь между компонентами нормально распределенного случайного вектора
Частным случаем статистической связи между количественными признаками x и y является корреляционная связь. При корреляционной связи от значения x факторного признака зависит лишь условное математическое ожидание M[Y | x] случайной величины Y, при этом все остальные характеристики распределения случайной величины Y остаются неизменными. Функция f(x), описывающая эту зависимость, называется функцией регрессии Y на X.
Частным случаем корреляционной связи между признаками x и y является линейная корреляционная связь, когда функция регрессии Y на X представляет собой линейную функцию:
$f(x)={{\beta }_{0}}+{{\beta }_{1}}x$.
Пусть случайный вектор $Z={{(X,Y)}^{T}}$ имеет двумерное нормальное распределение, $Z\sim{\ }N(m,C)$, где $m={{({{m}_{X}},{{m}_{Y}})}^{T}}$ – вектор математических ожиданий, $C=\left( \begin{matrix} \sigma _{X}^{2} & {{k}_{XY}} \\ {{k}_{YX}} & \sigma _{Y}^{2} \ \end{matrix} \right)$ – ковариационная матрица. Покажем, что если между случайными величинами X и Y есть статистическая связь, то такая связь является линейной корреляционной связью.
Запишем двумерную функцию плотности распределения случайного вектора Z в матричном виде:
${{f}_{Z}}(z)=\frac{1}{2\pi \sqrt{\det C}}\exp \left\{ -\frac{1}{2}{{(z-m)}^{T}}{{C}^{-1}}(z-m) \right\}$,
где $z={{(x,y)}^{T}}$. В скалярном виде:
${{f}_{XY}}(x,y)=\frac{1}{2{{\sigma }_{X}}{{\sigma }_{Y}}\sqrt{1-\rho _{XY}^{2}}}\exp \left\{ -\frac{1}{(1-\rho _{XY}^{2})}\times \right.$
|
$\left. \,\,\,\,\,\,\,\,\times \left[ \frac{{{(x-{{m}_{X}})}^{2}}}{2\sigma _{X}^{2}}-\rho _{XY}^{{}}\frac{(x-{{m}_{X}})(y-{{m}_{Y}})}{{{\sigma}_{X}}{{\sigma }_{Y}}}+\frac{{{(y-{{m}_{Y}})}^{2}}}{2\sigma _{Y}^{2}} \right] \right\}$, |
где ${{\rho }_{XY}}=\frac{{{k}_{XY}}}{{{\sigma }_{X}}{{\sigma }_{Y}}}$ – коэффициент корреляции.
Путём интегрирования по соответствующей переменной двумерной функции плотности (1) получим маргинальные распределения случайных величин X и Y:
|
${{f}_{X}}(x)=\int\limits_{-\infty }^{+\infty }{{{f}_{XY}}(x,y)dy}=\frac{1}{{{\sigma }_{X}}\sqrt{2\pi }}\exp \left\{ -\frac{{{(x-{{m}_{X}})}^{2}}}{2\sigma_{X}^{2}} \right\}$, |
|
${{f}_{Y}}(y)=\int\limits_{-\infty }^{+\infty }{{{f}_{XY}}(x,y)dx}=\frac{1}{{{\sigma }_{Y}}\sqrt{2\pi }}\exp \left\{ -\frac{{{(y-{{m}_{Y}})}^{2}}}{2\sigma_{Y}^{2}} \right\}$, |
Из равенств (1), (2) и (3) видно, что в случае если ${{\rho }_{XY}}=0$, выполняется тождество:
${{f}_{XY}}(x,y)={{f}_{X}}(x){{f}_{Y}}(y)$,
из которого следует, что если нормально распределённые случайные величины X и Y некоррелированы, то они независимы. Для произвольного закона распределения это утверждение в общем случае неверно.
По определению, условная плотность распределения случайной величины Y:
${{f}_{Y}}(y|x)=\frac{{{f}_{XY}}(x,y)}{{{f}_{X}}(x)}$.
Подставляя выражения (1 )и (2), получим
|
${{f}_{Y}}(y|x)=\frac{1}{{{\sigma }_{Y|X}}\sqrt{2\pi }}\exp \left\{ -\frac{{{(y-{{m}_{Y|X}}(x))}^{2}}}{2\sigma _{Y|X}^{2}} \right\}$, |
где использованы обозначения
|
${{m}_{Y|X}}(x)={{m}_{Y}}+\rho _{XY}^{{}}\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}(x-{{m}_{X}})$, |
|
${{\sigma }_{Y|X}}={{\sigma }_{Y}}\sqrt{1-\rho _{XY}^{2}}$. |
Из (4)–(6) следует, что при любом фиксированном значении x распределение случайной величины Y является нормальным распределением с постоянной дисперсией ${{\sigma }_{Y|X}}$. Это означает, что статистическая связь между величинами X и Y может быть только корреляционной. Покажем, что эта связь линейна.
Используя определения условного математического ожидания и среднеквадратичного отклонения, получим, что для случайной величины Y они равны соответственно ${{m}_{Y|X}}(x)$ и ${{\sigma }_{Y|X}}$:
|
$\text{M}[Y|x]=\int\limits_{-\infty }^{+\infty }{y{{f}_{Y}}(y|x)dy}={{m}_{Y|X}}(x)$, |
|
$\text{D}[Y|x]=\int\limits_{-\infty }^{+\infty }{{{\left( y-{{m}_{Y|X}}(x) \right)}^{2}}{{f}_{Y}}(y|x)dy}=\sigma _{Y|X}^{2}$. |
Учитывая линейную зависимость (5), заключаем, что функция регрессии Y на X является линейной. Это означает, что статистическая связь между нормально распределёнными случайными величинами может быть только линейной корреляционной. Из (5) получаем коэффициенты линейной регрессии:
|
${{\beta }_{0}}={{m}_{Y}}-\rho _{XY}^{{}}\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}{{m}_{X}}$, ${{\beta }_{1}}=\rho _{XY}^{{}}\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}$. |
Из этих равенств видно, что функция регрессии не зависит от x ( ${{\beta }_{1}}=0$ ), если коэффициент корреляции ${{\rho }_{XY}}=0$. Таким образом, некоррелированность нормально распределённых случайных величин означает отсутствие статистической связи между ними. Можно показать, что если $\left| {{\rho }_{XY}} \right|=1$, то между случайными величинами X и Y имеется линейная функциональная связь:
$Y=\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}X+\left( {{m}_{Y}}-\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}{{m}_{X}} \right)$.
Следовательно, коэффициент корреляции можно рассматривать как показатель тесноты статистической связи между нормально распределёнными случайными величинами X и Y.
На рисунке ниже показаны диаграммы рассеяния (в корреляционном анализе называемые корреляционными полями) двумерных нормальных распределений при различных значениях коэффициента корреляции.
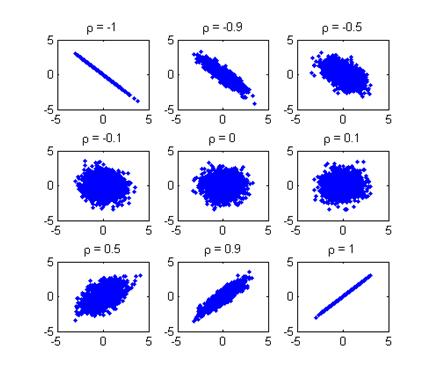
С изменением коэффициента корреляции от –1 до 1 прямая регрессии изменяет угол наклона, от минимального значения $-\arctan \left(\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}} \right)=-\frac{\pi }{4}$ до максимального $\arctan \left( \frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}\right)=\frac{\pi }{4}$, кроме того, изменяется степень рассеяния выборочных значений относительно прямой регрессии – при ${{\rho }_{XY}}=0$ рассеяние максимально, а при $\left| {{\rho }_{XY}} \right|=1$ рассеяние отсутствует.
Согласно (9), угол наклона линии регрессии зависит не только от коэффициента корреляции ${{\rho }_{XY}}$, но и от отношения с.к.о. $\frac{{{\sigma}_{Y}}}{{{\sigma }_{X}}}$. На рисунке ниже показаны корреляционные поля двумерных нормальных распределений при фиксированном значении коэффициента корреляции и различных значениях отношения $\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}$.
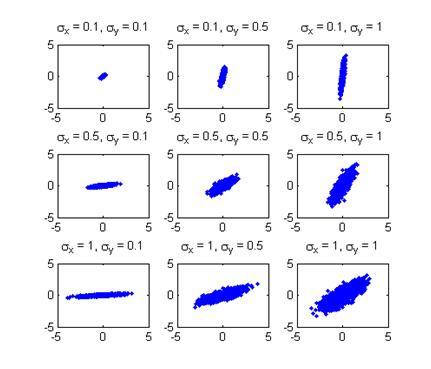
Из диаграмм рассеяния видно, что угол наклона прямой регрессии может изменяться практически от 0 до π/2 в зависимости от соотношения с.к.о. $\frac{{{\sigma }_{Y}}}{{{\sigma }_{X}}}$ при фиксированном значении коэффициента корреляции ρXY, кроме того, изменяется степень рассеяния выборочных значений относительно прямой регрессии, определяемая условными с.к.о. ${{\sigma }_{Y|X}}$ и ${{\sigma }_{X|Y}}$.
|
|
|









