Математическая статистика
![]() Анализ статистических взаимосвязей
Анализ статистических взаимосвязей
Ранговый коэффициент корреляции по Спирмену
Пусть x1,…,xn – выборка наблюдений случайной величины X, имеющей распределение ${{F}_{X}}(x)$, ${{x}_{(1)}},...,{{x}_{(n)}}$ – её вариационный ряд.
Рангом ri элемента xi выборки x1,…,xn называется его порядковый номер в вариационном ряду выборки, т.е.
${{x}_{({{r}_{i}})}}={{x}_{i}}$, $i=\overline{1,n}$.
Ранг ri элемента xi можно рассматривать как реализацию случайной величины ${{R}_{i}}={{R}_{i}}({{X}_{1}},...,{{X}_{n}})$, определяемой как ранг случайной величины Xi в случайной выборке X1,…,Xn.
Ранговой статистикой Z называется произвольная функция от рангов R1,…, Rn:
$Z=\varphi ({{R}_{1}},...,{{R}_{n}})$.
В связи с тем, что статистика Z является функцией случайных аргументов, Z является случайной величиной. Для каждой реализации x1,…,xn случайной выборки X1,…,Xn получим соответствующие ей реализацию рангов r1,…,rn и реализацию z ранговой статистики Z:
$z=\varphi ({{r}_{1}},...,{{r}_{n}})$.
Примечание. В случае если выборка x1,…,xn содержит одинаковые элементы, то им, как правило, приписывают одинаковый ранг, равный среднему из порядковых номеров этих элементов в вариационном ряду.
Пусть (x1, y1),…,(xn, yn) – выборка наблюдений двумерного случайного вектора (X, Y), имеющего распределение FXY(x, y); r1,…,rn – ранги элементов выборки x1,…,xn; s1,…,sn – ранги элементов выборки y1,…,yn.
Ранговым коэффициентом корреляции по Спирмену (Charles Spearman, 1904) называется ранговая статистика, определяемая следующим выражением:
|
$\rho_{XY}^{(sp)}=\frac{\sum\limits_{i=1}^{n}{({{R}_{i}}-\bar{r})({{S}_{i}}-\bar{s})}}{\sqrt{\sum\limits_{i=1}^{n}{({R_i}-\bar{r})^2}\sum\limits_{i=1}^{n}{(S_i-\bar{s})^2}}}$, |
где $\bar{r}$ и $\bar{s}$ – средние значения рангов:
|
$\bar{r}=\bar{s}=\frac{1}{n}\sum\limits_{i=1}^{n}{i}=\frac{n+1}{2}$. |
Выборочное значение этой статистики для выборки (x1, y1),…,(xn, yn) равно:
Фактически, значение рангового коэффициента корреляции по Спирмену для выборки (x1, y1),…,(xn, yn) – это значение линейного коэффициента корреляции для соответствующей выборки рангов (r1, s1),…,(rn, sn).
Учитывая (2), выражение (3) можно упростить:
|
$\tilde{\rho }_{XY}^{(sp)}=1-\frac{6}{n({{n}^{2}}-1)}\sum\limits_{i=1}^{n}{{{({{r}_{i}}-{{s}_{i}})}^{2}}}$. |
Известно, что линейный коэффициент корреляции ρXY используется для обнаружения линейной корреляционной связи между величинами X и Y. Так, если $|\rho _{XY}^{{}}|\ =1$, то между X и Y имеется линейная функциональная связь. Если ρXY = 0, то между X и Y отсутствует линейная корреляционная связь.
Значение $|\rho _{XY}^{(sp)}|\ =1$ будет означать, что между рангами R и S имеется линейная функциональная связь. Если же $\rho_{XY}^{(sp)}=0$, то между рангами R и S отсутствует линейная корреляционная связь.
Рассмотрим, что означают эти случаи в пространстве признаков X и Y. Если X и Y связаны линейной функциональной зависимостью $Y=aX+b$, то между рангами R и S также будет линейная зависимость. В самом деле, при $a>0$ бόльшим значениям X будут соответствовать бόльшие значения Y, таким образом, для отсортированной в порядке возрастания по X выборки (x1, y1),…,(xn, yn) соответствующая выборка рангов будет иметь вид:
ri |
1 |
... |
i |
... |
n |
si |
1 |
... |
i |
... |
n |
При $a<0$:
ri |
1 |
... |
i |
... |
n |
si |
n |
... |
n-i+1 |
... |
1 |
Рассчитывая ранговый коэффициент по формуле (4), получим, что при $a>0$: $\tilde{\rho }_{XY}^{(sp)}=1$, при $a<0$: $\tilde{\rho}_{XY}^{(sp)}=-1$.
Если $Y=\varphi (X)$, где φ(X) – монотонно возрастающая функция, то для отсортированной по X выборки (x1, y1),…,(xn, yn) соответствующая выборка рангов будет такой же, что и для случая линейной функциональной зависимости между X и Y при $a>0$. Если φ(X) – монотонно убывающая функция, то выборка рангов будет такой же, что и для случая линейной функциональной зависимости между X и Y при $a<0$.
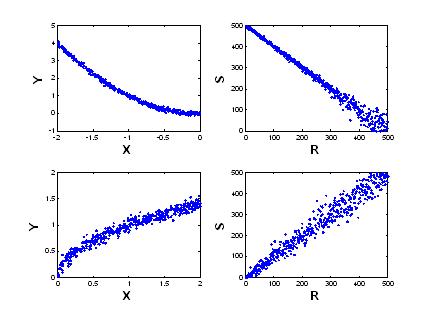
Из рисунка видно, что переход к рангам «выпрямляет» монотонную зависимость исходных признаков.
Рассмотрим другой случай, когда признаки X и Y независимы. В этой ситуации случайный вектор рангов $({{S}_{1}},...,{{S}_{n}})$, составленный для случайной выборки ${{Y}_{1}},...,{{Y}_{n}}$, соответствующей отсортированным по возрастанию значениям выборки ${{x}_{1}},...,{{x}_{n}}$, с равной вероятностью является любой из возможных n! перестановок, составленных из чисел 1,…,n. Следовательно, математическое ожидание рангового коэффициента корреляции по Спирмену (1) будет равно нулю, т.е. $\text{M}\left[ \rho _{XY}^{(sp)} \right]=0$. Можно показать, что дисперсия $\text{D}\left[ \rho _{XY}^{(sp)} \right]=\frac{1}{n-1}$. Это означает, что значения выборочного рангового коэффициента корреляции по Спирмену $\tilde{\rho }_{XY}^{(sp)}$ при условии независимости случайных величин X и Y и большом объёме выборки будут группироваться вблизи нуля.
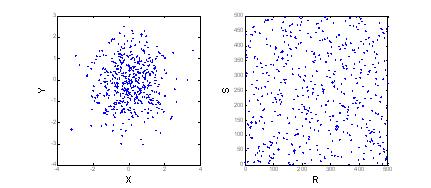
Из рисунка видно, что для независимых случайных величин X и Y выборочные ранги рассеяны практически равномерно внутри квадрата $n\times n$.
Для проверки значимости рангового коэффициента корреляции по Спирмену сформулируем основную гипотезу:
${{H}_{0}}:\rho _{XY}^{(sp)}=0$.
В качестве статистики критерия используют статистику:
$Z=\frac{\tilde{\rho }_{XY}^{(sp)}}{\sqrt{1-\tilde{\rho }_{XY}^{(sp)2}}}\sqrt{n-2}$,
которая при условии истинности H0 имеет распределение Стьюдента с n–2 степенями свободы: ${{f}_{Z}}(z|{{H}_{0}})\sim T(n-2)$.
Критическая область для статистики критерия выбирается, исходя из вида альтернативной гипотезы.
|
|
|









