Математическая статистика

Пример 1

По выборочным данным Примера 2* построить линейную регрессионную модель вида

$Y={{\beta }_{0}}+{{\beta }_{1}}x+{{\beta }_{2}}{{x}^{2}}+{{\beta }_{3}}{{x}^{3}}+\varepsilon (x)$,

где Y – среднее время решения вербальных заданий тестов, а регрессор – среднее время решения наглядно-образных заданий (случайная величина X), и проверить её значимость на уровне α = 0,1.

Решение

Из заданного вида регрессионной модели получаем, что вектор значений системы функций ${{\varphi }_{0}}(x),...,{{\varphi }_{k-1}}(x)$ в точке x имеет вид $\varphi (x)={{\left( 1,x,{{x}^{2}},{{x}^{3}} \right)}^{T}}$, число неизвестных параметров модели k = 4.

Запишем регрессионную матрицу F:

Дисперсионная матрица Фишера ${{({{F}^{T}}F)}^{-1}}$ имеет размерность 4*4 и равна

${{({{F}^{T}}F)}^{-1}}\approx \left( \begin{matrix} 150,5 & -21,0 & 0,91 & -0,01 \\ -21,0 & 2,96 & -0,13 & 0,002 \\ 0,91 & -0,13 & 0,006 & 0 \\ -0,01 & 0,002 & 0 & 0 \\ \end{matrix} \right)$.

По формуле (6) получаем точечную оценку вектора параметров модели:

$\tilde{\beta }={{\left( {\tilde\beta_0},{\tilde\beta_1},{\tilde\beta_2},{\tilde\beta_3} \right)}^{T}}\approx {{\left(-34,1;5,2;-0,18;0,0021 \right)}^{T}}$.

Таким образом, оценка функции регрессии имеет вид:

$\tilde{f}(x)=-34,1+5,2x-0,18{{x}^{2}}+0,0021{{x}^{3}}$.

Рассчитаем значения функции регрессии $\tilde{f}({{x}_{i}})$ в выборочных точках ${{x}_{1}},...,{{x}_{n}}$:

Показатели «эр-квадрат» и «эр-бар-квадрат» рассчитываем по формулам (1*) и (5*):

$R_{Y|X}^{2*}\approx 0,91$,

$\bar{R}_{Y|X}^{2}\approx 0,87$.

Сравнивая эти показатели с полученными в Примере 1*, делаем вывод, что рассматриваемая линейная модель обладает лучшими «объяснительными» возможностями, чем простейшая линейная регрессионная модель.

Визуальное представление выборочной функции регрессии и доверительных интервалов приведено на рис. 7.7.

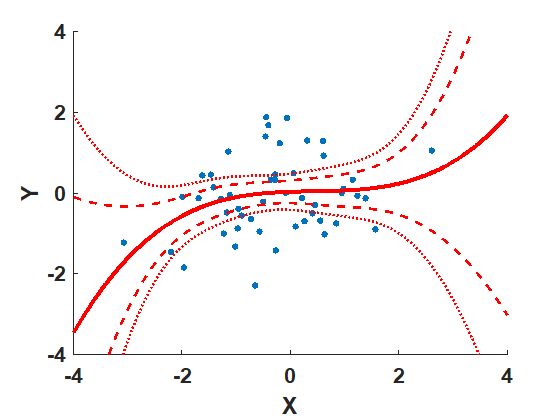
Рис. 7.7. Функция регрессии $\tilde{f}(x)=-34,1+5,2x-0,18{{x}^{2}}+0,0021{{x}^{3}}$

Для проверки гипотезы ${{H}_{0}}:{{\beta }_{1}}={{\beta }_{2}}={{\beta }_{3}}=0$ о незначимости регрессионной модели рассчитаем выборочное значение статистики Фишера (8):

$z=\frac{0,91/3}{{0,09}/{6}\;}\approx 20,2$,

которому соответствует значение p-value

$p=1-{{F}_{F(3,6)}}(20,2)\approx 0,0014$.

Согласно критерию проверки статистических гипотез, делаем вывод, что основная гипотеза должна быть отклонена, т.е. рассматриваемая линейная регрессионная модель значима.