Математическая статистика
![]() Анализ статистических взаимосвязей
Анализ статистических взаимосвязей
Корреляционное отношение
Если закон распределения случайного вектора $Z={{(X,Y)}^{T}}$ не является нормальным, то характер изменения условного математического ожидания $\text{M}[Y|x]=f(x)$ в общем случае является нелинейным, а условная дисперсия $\text{D}[Y|x]$ зависит от x. При каждом фиксированном x условная дисперсия $\text{D}[Y|x]$ является мерой рассеяния условного распределения ${{F}_{Y}}(y|x)$ относительно условного математического ожидания $\text{M}[Y|x]$, т.е. относительно значения функции регрессии в точке x.
Рассеяние случайной величины Y относительно её математического ожидания mY складывается из двух слагаемых, а именно: рассеяния случайной величины Y относительно функции регрессии и рассеяния значений функции регрессии относительно математического ожидания случайной величины Y, т.е.
|
$\text{M}[{{(Y-{{m}_{Y}})}^{2}}]=\text{M}[{{(Y-f(X))}^{2}}]+\text{M}[{{(f(X)-{{m}_{Y}})}^{2}}]$. |
Для доказательства преобразуем левую часть равенства:
$\text{M}[{{(Y-{{m}_{Y}})}^{2}}]=\text{M}\left[ {{\left( (Y-f(X))+(f(X)-{{m}_{Y}}) \right)}^{2}} \right]= $
$\ \ \ \ \ \ \ \ =\text{M}[{{(Y-f(X))}^{2}}]+2\text{M}[(Y-f(X))(f(X)-{{m}_{Y}})]+ $
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\text{M}[{{(f(X)-{{m}_{Y}})}^{2}}]$.
Учитывая, что
|
$\text{M}[(Y-f(X))(f(X)-{{m}_{Y}})]=0$, |
получаем верное равенство (1).
Величина ${{D}_{resY}}=\text{M}\left[ {{(Y-f(X))}^{2}} \right]$ характеризует степень разброса значений случайной величины Y относительно линии регрессии и называется остаточной дисперсией случайной величины Y (residual variance).
Величина ${{D}_{Y|X}}=\text{M}\left[ {{(f(X)-{{m}_{Y}})}^{2}} \right]$ характеризует степень разброса значений, принадлежащих линии регрессии, относительно математического ожидания случайной величины Y и называется дисперсией, обусловленной регрессией Y на X (variance explained by regression).
Таким образом, для общей дисперсии Y, дисперсии, обусловленной регрессией Y на X, и остаточной дисперсии Y справедливо правило сложения дисперсий:
${{D}_{Y}}={{D}_{resY}}+{{D}_{Y|X}}$.
Отношение дисперсии, обусловленной регрессией Y на X, к общей дисперсии случайной величины Y называется коэффициентом детерминации (КД) Y на X:
|
$R_{Y|X}^{2}=\frac{{{D}_{Y|X}}}{{{D}_{Y}}}$. |
Возможные значения КД $ 0\le R_{Y|X}^{2}\le 1$. КД показывает, какая доля в общей вариации результативного признака Y связана с вариацией линии регрессии. Иными словами, КД – это доля вариации, объяснённой регрессией, в общей вариации значений признака Y.
Отношение среднеквадратичного отклонения, обусловленного регрессией Y на X, к среднеквадратичному отклонению случайной величины Y называется корреляционным отношением (КО) Y на X:
$R_{Y|X}^{{}}=\sqrt{\frac{{{D}_{Y|X}}}{{{D}_{Y}}}}$.
Возможные значения КО $ 0\le R_{Y|X}^{{}}\le 1$. На основе КО судят о степени тесноты корреляционной связи между факторным признаком X и результативным признаком Y. Для характеристики степени тесноты связи может быть использована шкала Чеддока (табл. 6.3).
Равенство $R_{Y|X}^{{}}=0$ означает, что вариация значений функции регрессии f(x) при различных значениях x полностью отсутствует, линия регрессии является горизонтальной прямой ( $f(x)=const$ ). Другими словами, корреляционная связь между случайными величинами X и Y отсутствует.
Равенство $R_{Y|X}^{{}}=1$ будет иметь место, если остаточная дисперсия ${{D}_{resY}}=0$, т.е. если вариация признака Y относительно линии регрессии при каждом фиксированном значении x полностью отсутствует. Это означает, что при каждом значении x значение признака Y однозначно определено и равно f(x). Иными словами, между случайными величинами X и Y имеется функциональная связь.
Аналогично выражению (3) определяется КД $R_{X|Y}^{2}$ X на Y.
Между $R_{Y|X}^{2}$ и $R_{X|Y}^{2}$ в общем случае нет какой-либо простой зависимости. Возможны ситуации, когда один из этих показателей принимает нулевое значение, в то время как другой равен единице. Так, на рисунке ниже приведён пример ситуации, когда $R_{Y|X}^{2}\approx 1$, в то время как $R_{X|Y}^{2}\approx 0$. В первом случае (слева) линия регрессии Y на X является параболой (сплошная линия), разброс данных относительно неё небольшой, т.е. ${{D}_{resY}}\approx 0$, в то время как разброс значений, принадлежащих линии регрессии, относительно среднего значения случайной величины Y (горизонтальная пунктирная линия) много больше, т.е. ${{D}_{Y|X}}\approx {{D}_{Y}}$. Во втором случае (справа) линия регрессии X на Y – прямая, параллельная оси Y. Линия регрессия проходит на уровне среднего значения случайной величины X, т.е. ${{D}_{X|Y}}\approx 0$, в то время как разброс значений случайной величины X относительно линии регрессии практически равен разбросу относительно среднего значения случайной величины X, т.е. ${{D}_{resX}}\approx {{D}_{X}}$.
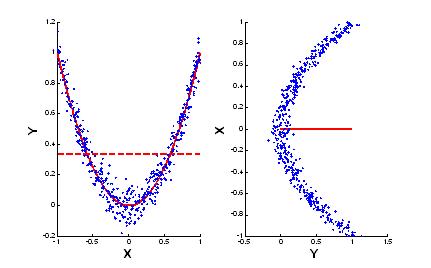
Иллюстрация к расчёту КД $R_{Y|X}^{2}$ и $R_{X|Y}^{2}$
Рассмотрим, как связаны между собой коэффициент корреляции ρXY и корреляционное отношение $R_{Y|X}^{{}}$. Из теории вероятностей известно, что из независимости случайных величин следует их некоррелированность. В терминах статистической связи это утверждение формулируется так: если между признаками отсутствует статистическая связь, то между ними отсутствует линейная корреляционная связь. Справедливость этого утверждения очевидна, поскольку линейная корреляционная связь – частный случай статистической связи. Обратное утверждение в общем случае неверно: отсутствие линейной корреляционной связи не означает отсутствие статистической связи какого-либо другого типа.
Ранее показано, что между компонентами двумерного нормально распределённого случайного вектора статистическая связь может быть лишь линейной корреляционной связью. Из этого следует, что термины «статистическая связь» и «линейная корреляционная связь» для нормального распределения эквивалентны. В теории вероятностей это утверждение известно как «из некоррелированности нормально распределённых случайных величин следует их независимость».
Рассчитаем КД для нормально распределённых случайных величин X и Y. По определению, коэффициент детерминации равен:
$R_{Y|X}^{2}=\frac{{{D}_{Y|X}}}{{{D}_{Y}}}=1-\frac{{{D}_{resY}}}{{{D}_{Y}}}=1-\frac{\text{M}\left[ {{(Y-f(X))}^{2}} \right]}{{{D}_{Y}}}$.
где $f(x)=\text{M}[Y|x]$ – функция регрессии.
Учитывая, что условная дисперсия ${{\sigma }_{Y|X}}$ не зависит от x:
$\text{D}[Y|x]=\text{M}\left[ {{(Y-f(x))}^{2}} \right]={{\sigma }_{Y}}\sqrt{1-\rho _{XY}^{2}}=\sigma _{Y|X}^{2}$,
запишем
$R_{Y|X}^{2}=1-\frac{\sigma _{Y|X}^{2}}{{{D}_{Y}}}=1-\frac{\sigma _{Y}^{2}\left( 1-\rho _{XY}^{2} \right)}{\sigma _{Y}^{2}}=\rho _{XY}^{2}$.
Таким образом, для нормально распределённых случайных величин коэффициент корреляции и корреляционное отношение совпадают с точностью до знака. Это означает, что использование корреляционного отношения в качестве показателя статистической связи имеет смысл лишь для признаков, распределения которых отличны от нормального. В случае же нормального распределения можно ограничиться рассмотрением лишь коэффициента корреляции.
При любом законе распределения случайного вектора $Z={{(X,Y)}^{T}}$ для КД и коэффициента корреляции справедливо неравенство:
$ 0\le \rho _{XY}^{2}\le R_{Y|X}^{2}\le 1$.
При этом возможны следующие варианты:
а) $\rho _{XY}^{2}=0$ тогда и только тогда, когда линейная корреляционная связь между X и Y отсутствует;
б) $\rho _{XY}^{2}=R_{Y|X}^{2}=1$ тогда и только тогда, когда имеется линейная функциональная связь между X и Y;
в) $\rho _{XY}^{2}<R_{Y|X}^{2}=1$ тогда и только тогда, когда имеется нелинейная функциональная связь между X и Y;
г) $\rho _{XY}^{2}=R_{Y|X}^{2}<1$ тогда и только тогда, когда регрессия Y на X линейна, но функциональная связь отсутствует.
|
|
|









