Математическая статистика

Далее будем рассматривать лишь случай простой основной статистической гипотезы. Алгоритм проверки любой простой гипотезы включает следующие этапы.

1) Сформулировать проверяемую гипотезу H₀ и альтернативную гипотезу H’. Гипотезы формулируются, исходя из условия задачи или особенностей рассматриваемой проблемной области.

2) Выбрать уровень значимости α, на котором будет сделано статистическое решение. Уровень значимости выбирается исследователем как допустимая вероятность ошибки первого рода при принятии статистического решения. Обычно, уровень значимости выбирается небольшим, например, α = 0,1 или α = 0,01, однако, следует помнить, что выбор слишком малого уровня значимости приведёт к увеличению вероятности ошибки второго рода при принятии статистического решения.

3) Выбрать статистику критерия Z для проверки гипотезы H₀. Для большинства встречающихся на практике статистических гипотез H₀ выражение для статистики критерия Z, обеспечивающей минимальное или близкое к минимальному значение вероятности ошибки второго рода при фиксированном уровне значимости, известно. От исследователя, как правило, не требуется придумывать оригинальное выражение для используемой статистики критерия.

4) Найти закон распределения ${{f}_{Z}}(z|{{H}_{0}})$ выбранной статистики критерия Z при условии истинности основной гипотезы H₀. Законы распределения большинства используемых на практике статистик критерия также известны.

5) Построить область допустимых значений Ω₀ и критическую область Ω’. Критическая область Ω’ зависит от вида статистики критерия Z, альтернативной гипотезы H’ и уровня значимости α.

Простая основная параметрическая гипотеза имеет вид ${{H}_{0}}:\theta ={{\theta }_{0}}$, где θ – неизвестный параметр генеральной совокупности, θ₀ – некоторая константа из области возможных значений параметра θ. Для такой основной гипотезы возможны следующие варианты формулировок альтернативных гипотез:

а) $H':\theta <{{\theta }_{0}}$;

б) $H':\theta >{{\theta }_{0}}$;

в) $H':\theta \ne {{\theta }_{0}}$.

Как правило, оптимальная критическая область – это область маловероятных значений статистики критерия в хвостах распределения. Если критическая область расположена в левом хвосте распределения ${{f}_{Z}}(z|{{H}_{0}})$, то такая критическая область называется левосторонней, если в правом хвосте – то правосторонней, если в обоих хвостах – то двусторонней. В случае двусторонней критической области площади каждого из хвостов, как правило, выбираются равными.

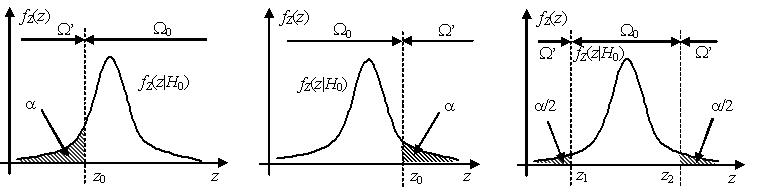
Уровень значимости α определяет ширину критической области.

6) Вычислить выборочное значение статистики критерия z на основе имеющихся выборочных наблюдений из генеральной совокупности.

7) Принять статистическое решение, используя решающее правило: если выборочное значение статистики критерия $z\in {{\Omega }_{0}}$, то основная гипотеза H₀ принимается, если выборочное значение статистики критерия $z\in \Omega '$, то основная гипотеза H₀ отвергается в пользу альтернативной гипотезы H’.

Иногда при использовании статистических пакетов для проверки гипотез процедура статистического анализа не возвращает в явном виде выборочное значение z статистики критерия Z. В этом случае статистическое решение принимается на основе так называемого значения p-value.

Если альтернативная гипотеза имеет вид $H':\theta <{{\theta }_{0}}$ или $H':\theta >{{\theta }_{0}}$, то значение p-value – это площадь под графиком функции плотности распределения статистики критерия, расположенная левее / правее выборочного значения статистики критерия z:

$H':\theta <{{\theta }_{0}}\ \Rightarrow \ p={{F}_{Z}}(z), $

$H':\theta >{{\theta }_{0}}\ \Rightarrow \ p=1-{{F}_{Z}}(z). $

Иными словами, p-value – это вероятность того, что статистика критерия Z примет более «экстремальные» значения в левом / правом хвосте критической области, чем рассчитанное по выборке выборочное значение z.

Если альтернативная гипотеза имеет вид $H':\theta \ne {{\theta }_{0}}$, то p-value рассчитывается по следующей формуле:

$H':\theta \ne {{\theta }_{0}}\ \Rightarrow \ p=\min \left( {{F}_{Z}}(z),1-{{F}_{Z}}(z) \right)/2$.

В этом случае p-value – это вероятность того, что статистика критерия Z примет более «экстремальные» значения, чем z, в любом из хвостов двусторонней критической области.

Если значение p-value мало, это свидетельствует о том, что выборочное значение статистики критерия z уже приняло довольно «экстремальное» значение, что может говорить о противоречии выборочных данных основной гипотезе. Если значение p‑value велико, то оснований отвергать основную гипотезу нет.

При использовании значения p-value критерий проверки статистической гипотезы формулируется следующим образом: если значение p-value больше уровня значимости a, то основная гипотеза H₀ принимается, если значение p‑value меньше уровня значимости a, то основная гипотеза H₀ отвергается.

Если основная гипотеза H₀ отвергается, то делается вывод, что выборочные наблюдения противоречат основной гипотезе, если же H₀ принимается, то выборочные данные могли быть получены из генеральной совокупности со свойствами, указанными в H₀, что, впрочем, не означает, что генеральная совокупность в самом деле имеет эти свойства.

Пример 1