Математическая статистика

В практических задачах часто требуется проверить то или иное предположение относительно каких-нибудь свойств закона распределения наблюдаемой случайной величины X. Для проверки этого предположения исследователь проводит эксперимент, в результате которого получает реализацию x₁,...,x_n случайной выборки X₁,...,X_n из генеральной совокупности X. По этим данным ему нужно дать ответ на вопрос: согласуется ли его гипотеза с результатами эксперимента или нет? Другими словами, исследователю нужно решить, можно ли принять выдвинутую гипотезу или её нужно отклонить как противоречащую результатам эксперимента.

Любое предположение относительно параметров или закона распределения наблюдаемой случайной величины (или нескольких величин) называется статистической гипотезой. Проверяемую статистическую гипотезу также называют основной, или нулевой, статистической гипотезой и, как правило, обозначают H₀.

Наряду с проверяемой статистической гипотезой H₀ выдвигают также конкурирующую гипотезу, противоречащую H₀. Конкурирующая гипотеза называется альтернативной и, как правило, обозначается H₁ или H’. Если в результате статистического анализа делается вывод, что основная гипотеза H₀ должна быть отвергнута, то решение принимается в пользу альтернативной гипотезы H’. В простейшем случае альтернативная гипотеза – это отрицание основной гипотезы.

Статистическая гипотеза H₀ называется простой, если она однозначно определяет параметр или распределение наблюдаемой случайной величины X. В противном случае гипотеза H₀ называется сложной.

Если статистическая гипотеза H₀ представляет собой утверждение о некотором параметре q известного распределения случайной величины X, то гипотеза называется параметрической. В противном случае гипотеза называется непараметрической.

Пример 1

Пример 2

Статистическое решение, т.е. решение о принятии или отклонении основной гипотезы H₀, проводится в соответствии с некоторым критерием.

Статистическим критерием, или решающим правилом, при проверке статистической гипотезы H₀ называется правило, в соответствии с которым гипотеза H₀ принимается или отвергается.

Статистическая гипотеза – это всегда утверждение о свойствах наблюдаемой генеральной совокупности, а задача проверки статистической гипотезы состоит в проверке соответствия результатов эксперимента x₁,...,x_n выдвинутой гипотезе. Иными словами, задача проверки статистической гипотезы состоит в ответе на вопрос: могло ли случиться так, что выборка x₁,..., x_n была получена из генеральной совокупности с указанными в гипотезе свойствами?

Как правило, статистический критерий связывают с некоторой статистикой Z, являющейся функцией случайной выборки X₁,...,X_n. Эта статистика служит мерой, насколько наблюдаемые выборочные значения могли быть получены из генеральной совокупности с указанными в основной гипотезе свойствами. Вопрос о том, какую статистику Z следует взять для проверки той или иной статистической гипотезы, не имеет однозначного ответа. Это может быть любая статистика, удовлетворяющая следующим требованиям:

1) закон распределения F_Z(z | H₀) при условии истинности основной гипотезы H₀ должен быть известен;

2) закон распределения должен быть чувствителен к факту справедливости основной или альтернативной гипотезы, т.е. законы распределения F_Z(z | H₀) и F_Z(z | H’) должны существенно различаться.

Для реализации x₁,...,x_n случайной выборки X₁,...,X_n, статистика Z примет реализацию z. Предположим, что гипотеза H₀ верна. В связи с тем, что закон распределения статистики Z при условии истинности основной гипотезы H₀ известен, то возможно рассчитать вероятность её попадания в некоторую окрестность точки z. Если эта вероятность высока, это означает, что ничто не противоречит предположению об истинности гипотезы H₀. Если же эта вероятность мала или близка к нулю, то это может означать один из двух вариантов:

1) в условиях основной гипотезы H₀ произошло практически невозможное событие;

2) статистика Z на самом деле имеет некоторый другой закон распределения, отличный от F_Z(z | H₀), при котором вероятность её попадания в окрестность точки z много больше нуля. Это означает, что предположение об истинности гипотезы H₀ сделано неверно.

Статистика $ Z=Z({{X}_{1}},...,{{X}_{n}}) $, на основе реализации которой $z=Z({{x}_{1}},...,{{x}_{n}})$ выдвигается статистическое решение, называется статистикой критерия (test statistics). Реализация статистики критерия $z=Z({{x}_{1}},...,{{x}_{n}})$, рассчитанная для выборки x₁,...,x_n, называется выборочным значением статистики критерия.

Проверка статистических гипотез основывается на принципе, в соответствии с которым маловероятные события относительно статистики критерия Z считаются невозможными. В соответствии с этим принципом, если вероятность попадания статистики критерия Z в окрестность рассчитанного выборочного значения z мала, то должен выбираться вариант 2), т.е. основная гипотеза H₀ отклоняется.

Область Ω₀ наиболее вероятных значений статистики критерия Z, при попадании выборочных значений z в которую основная гипотеза H₀ принимается, называется областью допустимых значений статистики критерия Z.

Область Ω’ маловероятных значений статистики критерия Z, при попадании выборочных значений z которую основная гипотеза H₀ отклоняется, называется критической областью значений статистики критерия Z. Множество ${{\Omega }_{0}}\cup \Omega '$ должно являться множеством всех возможных значений статистики критерия Z.

Из определений области допустимых значений и критической области следует статистический критерий проверки гипотезы H₀: если выборочное значение статистики критерия $z\in {{\Omega }_{0}}$, то основная гипотеза H₀ принимается, если выборочное значение статистики критерия $z\in \Omega '$, то основная гипотеза H₀ отвергается.

Пусть для выборки x₁,...,x_n статистика критерия Z приняла выборочное значение z, лежащее в критической области Ω’, т.е. вероятность попадания статистики критерия Z в окрестность которой мала. В соответствии со статистическим критерием основная гипотеза H₀ должна быть отвергнута. Однако событие $z\in \Omega '$, хоть и с малой вероятностью, но всё же могло произойти в условиях основной гипотезы H₀. Если это так, то статистическое решение об отклонении гипотезы H₀ будет ошибочным.

С другой стороны, если для выборки x₁,...,x_n статистика критерия Z приняла выборочное значение z, лежащее в области допустимых значений Ω₀, это могло случиться как в условиях основной гипотезы H₀ (с высокой вероятностью), так и, возможно, в условиях альтернативной гипотезы H’ (с низкой вероятностью). В соответствии со статистическим критерием основная гипотеза H₀ принимается. Если же событие $z\in {{\Omega }_{0}}$ на самом деле произошло в условиях альтернативной гипотезы H’, то статистическое решение о принятии гипотезы H₀ также будет ошибочным. В обоих случаях говорят об ошибках принятия статистического решения.

Ошибкой 1-го рода при принятии статистического решения называется событие, состоящее в том, что основная гипотеза H₀ отвергается, в то время как она верна.

Ошибкой 2-го рода при принятии статистического решения называется событие, состоящее в том, что основная гипотеза H₀ принимается, в то время как верна альтернативная гипотеза H’.

Пример 3

Пример 4

Уровнем значимости α при проверке статистической гипотезы называется вероятность ошибки первого рода:

$\alpha =P\left( Z\in \Omega '|{{H}_{0}} \right)$.

Вероятность β ошибки второго рода:

$\beta =P\left( Z\in {{\Omega }_{0}}|H' \right)$.

Ясно, что с уменьшением вероятности ошибки первого рода возрастает вероятность ошибки второго рода и наоборот. Это означает, что при выборе критической области и области допустимых значений статистики критерия должен достигаться определённый компромисс.

Проиллюстрируем сказанное на примере. Пусть основная и альтернативная гипотезы H₀ и H’ являются простыми. Пусть статистики критерия Z при условии истинности основной гипотезы H₀ имеет нормальное распределение ${{F}_{Z}}(z|{{H}_{0}})\sim N({{m}_{1}},{{\sigma }_{1}})$, а при условии истинности H’ – распределение ${{F}_{Z}}(z|{{H}_{0}})\sim N({{m}_{2}},{{\sigma }_{2}})$.

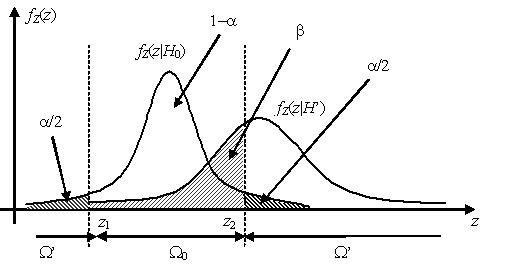
У качестве критической области Ω’ выбраны хвосты распределения ${{f}_{Z}}(z|{{H}_{0}})$, площадь каждого из которых равна α/2. Вероятность попадания статистики критерия Z, имеющей распределение ${{f}_{Z}}(z|{{H}_{0}})$, в критическую область, таким образом, равна вероятности ошибки первого рода α. Вероятность ошибки второго рода β равна площади под графиком функции плотности распределения ${{f}_{Z}}(z|H')$ внутри области допустимых значений Ω₀. Из графиков видно, что уменьшая ширину области допустимых значений, площадь a будет увеличиваться, в то время как площадь β – уменьшаться, и наоборот.

Точки на оси значений статистики критерия z, разделяющие область допустимых значений Ω₀ и критическую область Ω’, называются критическими точками. На рисунке выше это точки z₁ и z₂, являющиеся квантилями распределения ${{f}_{Z}}(z|{{H}_{0}})$ на уровнях α/2 и 1 – α/2 соответственно.

В случае если основная и альтернативная гипотезы H₀ и H’ являются простыми, величина μ = 1 – β называется мощностью критерия.

Очевидно, что при заданном значении вероятности ошибки первого рода a выбор критической области Ω’ может быть сделан неоднозначно. Единственное требование, предъявляемое к критической области, состоит в том, что площадь под графиком известного распределения статистики критерия ${{f}_{Z}}(z|{{H}_{0}})$ в критической области должна быть равна α. Однако соответствующие различным критическим областям критерии будут иметь, вообще говоря, различные вероятности β ошибок второго рода.

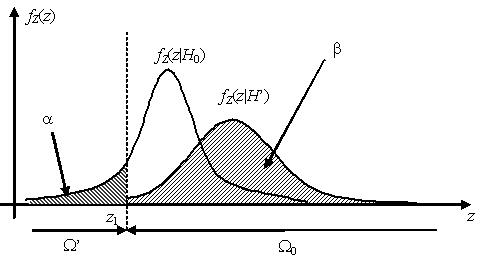
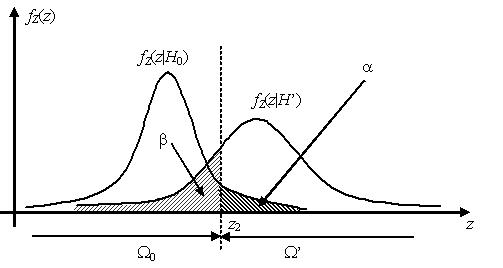
Наилучшей критической областью (НКО) называют критическую область, которая при заданном уровне значимости a обеспечивает минимальную вероятность β ошибки второго рода. Критерий, использующий наилучшую критическую область, имеет максимальную мощность.

Если альтернативная гипотеза является сложной, т.е. не определяет однозначно функцию распределения F_X(x) генеральной совокупности X, а следовательно, и функцию распределения статистики критерия ${{F}_{Z}}(z|H')$, а определяет её с точностью до значения некоторого параметра θ, то вводят функцию мощности критерия μ(θ) как функцию параметра θ. Значение функции мощности критерия μ(θ) в точке θ определяется как

$\mu (\theta )=1-\beta (\theta )$,

где β(θ) – вероятность ошибки второго рода при условии, что неизвестный параметр принял значение θ, θ∈Θ, где Θ – область возможных значений параметра θ.

Пример 5

Функция мощности имеет важное значение в задачах, связанных с оценкой необходимого объёма выборки для обеспечения требуемой вероятности ошибки второго рода принятия статистического решения при заданной вероятности ошибки первого рода.