Математическая статистика

Пример 1

Проводятся наблюдения числа посетителей развивающегося сайта (признак X) и его средневзвешенной позиции по основным запросам в поисковой системе (признак Y). В результате наблюдения получены следующие данные.

Рассчитать коэффициент корреляции между указанными признаками и ответить на вопрос: можно ли утверждать, что между числом посетителей сайта и его средневзвешенной позицией в поисковой системе есть значимая (α = 0,1) линейная корреляционная связь?

Решение

Для предварительного анализа данных построим корреляционное поле имеющихся наблюдений (рис. 6.4). Уже по виду корреляционного поля иногда можно сделать вывод о наличии и характере связи между признаками X и Y. Так, из рисунка видно, что некоторая нелинейная зависимость (например, квадратичная) лучше описывает имеющиеся данные, чем линейная зависимость, измеряемая коэффициентом корреляции.

Рассчитаем точечную оценку коэффициента корреляции по формуле (1):

$\bar{x}=\frac{1}{8}(500+...+1630)=1474;$

$\bar{y}=\frac{1}{8}(12,2+...+5,5)=7;$

$\sigma _{X}^{*}=\sqrt{\frac{1}{8}\left( {{(500-1474)}^{2}}+...+{{(1630-1474)}^{2}} \right)}\approx 668;$

$\sigma _{Y}^{*}=\sqrt{\frac{1}{8}\left( {{(12,2-7)}^{2}}+...+{{(5,5-7)}^{2}} \right)}\approx 2,7;$

$k_{XY}^{*}=\frac{1}{8}\left( (500-1474)(12,2-7)+...+(1630-1474)(5,5-7) \right)\approx -1670;$

$\rho _{XY}^{*}=\frac{-1670}{668\cdot 2,7}\approx -0,94.$

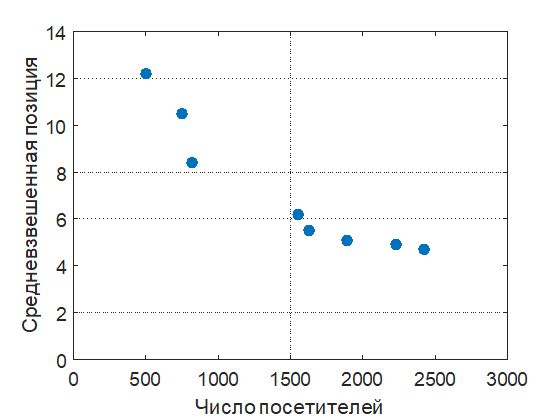
Рис. 6.4. Корреляционное поле

Рассчитанная точечная оценка коэффициента корреляции говорит о сильной линейной корреляционной связи. Однако вследствие небольшого объёма выборки и смещённости этой оценки, значение коэффициента корреляции ρ_XY генеральной совокупности может существенно отличаться от значения рассчитанной оценки $\rho _{XY}^{*}$.

Найдём границы доверительного интервала для ρ_XY. Учитывая небольшой объём выборки, используем формулу (2):

$\underline{\rho}_{XY}=\tanh \left( \frac{1}{2}\ln \frac{0,06}{1,94}+\frac{-0,94}{14}-\frac{1,64}{2,34} \right)\approx \tanh(-2,5)\approx -0,987;$

$\bar{\rho }_{XY}^{{}}=\tanh \left( \frac{1}{2}\ln \frac{0,06}{1,94}+\frac{-0,94}{14}+\frac{1,64}{2,34} \right)\approx \tanh (-1,1)\approx -0,802;$

где ${{u}_{0,95}}=1,64$ – квантиль стандартного нормального распределения на уровне 1–α/2.

Для проверки гипотезы о значимости коэффициента корреляции ${{H}_{0}}:{{\rho }_{XY}}=0$ против альтернативной гипотезы $H':{{\rho }_{XY}}<0$ рассчитаем выборочное значение статистики критерия по формуле (3):

$z=\frac{-0,94\cdot 2,45}{\sqrt{1-{{0,94}^{2}}}}\approx -6,74$ ,

которому соответствует значение p-value

$p={{F}_{T(6)}}(-6,45)\approx 0,00026$.

Согласно критерию проверки статистических гипотез, делаем вывод, что основная гипотеза должна быть отклонена, т.е. линейная корреляционная связь между рассматриваемыми признаками значима.