Математическая статистика

Пусть X₁,…,X_n – случайная выборка объёма n из генеральной совокупности X с функцией распределения F_X(x; θ), зависящей от параметра θ, значение которого неизвестно. Наиболее простым и популярным методом построения доверительного интервала (θ₁; θ₂) для неизвестного параметра θ является метод, основанный на использовании так называемой центральной статистики.

Центральной статистикой случайной выборки X₁,…,X_n называется любая статистика $Z=Z({{X}_{1}},...,{{X}_{n}};\theta )$, зависящая от неизвестного параметра θ, удовлетворяющая следующим свойствам:

1. закон распределения F_Z(z) статистики Z известен и не зависит от θ;

2. статистика Z непрерывна и строго монотонна по θ.

Из определения квантиля следует, что для любой случайной величины, в том числе, и для статистики $Z=Z({{X}_{1}},...,{{X}_{n}};\theta )$ справедливо равенство:

где ${{z}_{\alpha /2}}$ и ${{z}_{1-\alpha /2}}$ – квантили случайной величины Z на уровнях α/2 и (1­–α/2) соответственно.

При построении односторонних доверительных интервалов рассматриваются другие равенства:

Задача нахождения доверительного интервала состоит в разрешении неравенства, стоящего под знаком вероятности в выражении (1) (или выражениях (2), (3)), относительно неизвестного параметра θ. В результате получим эквивалентное выражение:

$P\left( {{\theta }_{1}}({{X}_{1}},...,{{X}_{n}})<\theta <{{\theta }_{2}}({{X}_{1}},...,{{X}_{n}}) \right)=1-\alpha $,

из которого следует, что интервал $\left( {{\theta }_{1}}({{X}_{1}},...,{{X}_{n}});{{\theta }_{2}}({{X}_{1}},...,{{X}_{n}}) \right)$ является доверительным.

Таким образом, алгоритм построения доверительного интервала для неизвестного параметра θ на основе случайной выборки X₁,…,X_n состоит в следующем.

1. Выбор центральной статистики $Z=Z({{X}_{1}},...,{{X}_{n}};\theta )$ и определение её закона распределения F_Z(z). Знание закона распределения необходимо для расчёта квантилей ${{z}_{\alpha /2}}$ и ${{z}_{1-\alpha /2}}$ (или z_α и z_1-α).

2. Разрешение неравенства под знаком вероятности в выражении (1) (или выражениях (2), (3)) относительно θ.

Очевидно, что для случайной выборки X₁,…, X_n в общем случае может быть построено бесконечно много центральных статистик Z. Возникает вопрос, какую центральную статистику выбрать, чтобы полученный с её помощью доверительный интервал был бы наиболее узким, а следовательно, наиболее точным, при фиксированной доверительной вероятности $\gamma =1-\alpha $?

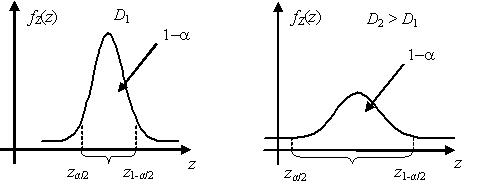
Как правило, центральные статистики связывают с некоторой точечной оценкой $\tilde{\theta }$ неизвестного параметра θ. Чем меньше дисперсия точечной оценки $\tilde{\theta }$, тем меньшей дисперсией будет обладать и центральная статистика Z, построенная на основе $\tilde{\theta }$. А для случайной величины с меньшей дисперсией интервал $({{z}_{\alpha /2}};{{z}_{1-\alpha /2}})$ будет ýже при прочих равных условиях. Учитывая монотонность зависимости центральной статистики Z от параметра θ, заключаем, что чем ýже интервал $({{z}_{\alpha /2}};{{z}_{1-\alpha /2}})$, тем ýже доверительный интервал (θ₁; θ₂). Таким образом, из вышесказанного следует, что центральную статистику $Z({{X}_{1}},...,{{X}_{n}};\theta )$ целесообразно выбирать связанной с эффективной оценкой $\tilde{\theta}({{X}_{1}},...,{{X}_{n}})$ неизвестного параметра θ.

Пример 1