Математическая статистика

Пусть x₁,…,x_n – выборка наблюдений случайной величины X, имеющей распределение F_X(x). Пусть выборка содержит k вариантов z₁,…,z_k, причём вариант z_i встречается с частотой n_i, $i=\overline{1,k}$.

Введём случайную величину дискретного типа $X_{n}^{*}$, принимающую значения z₁,…,z_k с вероятностями, равными соответствующим относительным частотам n₁/n,…,n_k/n, т.е. $P(X_{n}^{*}={{x}_{i}})={{n}_{i}}/n$, $i=\overline{1,k}$. Относительные частоты принадлежат отрезку [0; 1], причём их сумма равна единице, т.е. для относительных частот выполнены все требования, предъявляемые к вероятности распределения. Распределение случайной величины $X_{n}^{*}$ называется распределением выборки x₁,…,x_n (табл. 1.3).

Таблица 1.3

Распределение выборки

В связи с тем, что в выборке может присутствовать лишь конечное (или счётное) число вариантов наблюдаемой случайной величины X, распределение случайной величины $X_{n}^{*}$ всегда является дискретным.

Функция распределения случайной величины $X_{n}^{*}$ называется эмпирической (выборочной) функцией распределения (ЭФР ) и обозначается $F_{n}^{*}(x)$:

$F_{n}^{*}(x)={{F}_{X_{n}^{*}}}(x)=P(X_{n}^{*}<x)=\sum\limits_{{{z}_{i}}<x}{\frac{{{n}_{i}}}{n}}=\frac{1}{n}\sum\limits_{{{z}_{i}}<x}{{{n}_{i}}}$.

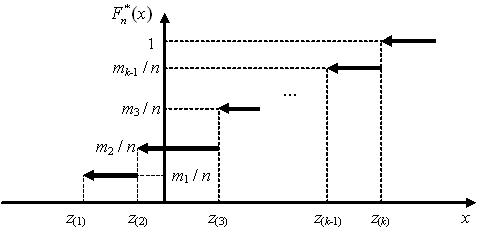
Как известно, функция распределения случайной величины дискретного типа представляет собой кусочно-постоянную функцию. График ЭФР для выборки x₁,…,x_n с вариантами z₁,…,z_k приведён на рисунке ниже. Несложно показать, что ЭФР может принимать лишь значения, равные накопленным относительным частотам вариантов z₁,…,z_k либо равняться нулю:

В точках z₁,…,z_k ЭФР претерпевает разрыв непрерывности и является, как и любая функция распределения, непрерывной слева.

Поскольку ЭФР выборки x₁,…,x_n является функцией распределения дискретной случайной величины $X_{n}^{*}$, то для неё справедливы все свойства функции распределения дискретной случайной величины.

Эмпирическую функцию распределения $F_{n}^{*}(x)$ выборки x₁,…,x_n можно рассматривать как реализацию случайной эмпирической функции распределения $\mathcal{F}_{n}^{*}(x)$ соответствующей случайной выборки X₁,…,X_n. При каждой конкретной реализации случайной выборки получаем соответствующую ей реализацию случайной ЭФР.

Пример 1

Выборочными (эмпирическими) числовыми характеристиками называются числовые характеристики случайной величины $X_{n}^{*}$. К таким характеристикам относятся, например, моменты случайной величины. Напомним, что зная функцию распределения f_X(x) случайной величины X (или распределение вероятностей p₁,…,p_k для случайной величины дискретного типа), математическое ожидание элементарной действительной функции ξ(X) случайной величины X рассчитывается по формулам:

$\text{M}[\xi (X)]=\int\limits_{-\infty }^{\infty }{\xi (x)f(x)dx}$

и

для непрерывного и дискретного случаев соответственно.

Учитывая (2), запишем выражение для расчёта выборочного начального момента r-го порядка. Все выборочные числовые характеристики будем обозначать с верхним знаком «звёздочки»:

В связи с тем, что каждый вариант z_i встречается в выборке x₁,…,x_n с соответствующей частотой n_i, $i=\overline{1,k}$, каждое произведение $z_{i}^{r}{{n}_{i}}$ может быть записано как сумма n_i одинаковых элементов выборки, равных варианту z_i. Таким образом, выражение (3) примет вид:

Выражение (3) называется взвешенной формой записи выборочного начального момента r-го порядка, а выражение (4) – невзвешенной.

Взвешенная форма записи выборочного начального момента r-го порядка представляет собой среднее арифметическое различных элементов (вариантов) выборки, возведённых в r-ю степень и взвешенных их частотами. Из невзвешенной формы записи видно, что выборочный начальный момент r-го порядка представляет собой простое среднее арифметическое элементов выборки, возведённых в r-ю степень. В связи с этим нередко выборочный начальный момент r-го порядка обозначается через $\overline{{{x}^{r}}}$.

Выборочный начальный момент первого порядка $\alpha _{1}^{*}$ называется выборочным математическим ожиданием и представляет собой простое среднее арифметическое элементов выборки, в связи с чем нередко обозначается через $\bar{x}$:

Нижний индекс ‘_X’ в обозначении выборочного математического ожидания и других выборочных характеристик определяется случайной величиной, наблюдениями которой являются рассматриваемые выборочные значения x₁,…,x_n.

Операция центрирования выборки состоит в смещении её значений на $\bar{x}$:

${{\varepsilon }_{i}}={{x}_{i}}-\bar{x},\ \ \ i=\overline{1,n}$.

Выборочное математическое ожидание (среднее) центрированной выборки ε₁,…,ε_n равно нулю:

$\bar{\varepsilon }=\frac{1}{n}\sum\limits_{i=1}^{n}{{{\varepsilon}_{i}}}=\frac{1}{n}\sum\limits_{i=1}^{n}{({{x}_{i}}-\bar{x})}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{x}_{i}}}-\bar{x}=0$.

Учитывая определение центрального момента r-го порядка случайной величины дискретного типа, запишем выражение для расчёта выборочного центрального момента r-го порядка:

Выражение (6) является взвешенной формой записи. Невзвешенная форма получается из взвешенной заменой произведений ${{({{z}_{i}}-\bar{x})}^{r}}{{n}_{i}}$, $i=\overline{1,k}$, на сумму n_i одинаковых слагаемых:

$\mu _{r}^{*}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{({{x}_{i}}-\bar{x})}^{r}}}$.

Выборочный центральный момент второго порядка $\mu _{2}^{*}$ называется выборочной дисперсией:

Выборочная дисперсия является мерой рассеяния выборочных значений x₁,…,x_n относительно их среднего арифметического $\bar{x}$.

Выборочное среднеквадратичное отклонение (с.к.о.) $\sigma _{X}^{*}$ выборки x₁,…,x_n определяется как квадратный корень из выборочной дисперсии $d_{X}^{*}$:

$\sigma _{X}^{*}=\sqrt{d_{X}^{*}}$.

Для выборочных начального и центрального моментов применимы все тождества, справедливые для начального и центрального моментов случайной величины дискретного типа. В частности, полезное на практике соотношение между выборочной дисперсией и выборочным начальным моментом второго порядка:

Это равенство следует читать как «выборочная дисперсия равна разности между средним квадратом и квадратом среднего».

Выборочный коэффициент асимметрии $\gamma _{X}^{*}$ (skewness) и выборочный эксцесс $\varepsilon _{X}^{*}$ (kurtosis) – это коэффициент асимметрии и эксцесс случайной величины $X_{n}^{*}$:

$\gamma _{X}^{*}=\frac{\mu _{3}^{*}}{{{(\sigma _{X}^{*})}^{3}}}$,

$\varepsilon _{X}^{*}=\frac{\mu _{4}^{*}}{{{(\sigma _{X}^{*})}^{4}}}-3$,

Выборочный коэффициент асимметрии характеризует степень асимметрии, а эксцесс – степень «плосковершинности» распределения выборки.

Пример 2

Выборочные характеристики могут быть рассчитаны для группированной выборки. Пусть проведена группировка выборочных данных x₁,…,x_n на k интервалов [α₀; α₁), [α₁; α₂),…, [α_k-1; α_k]; n_i – частота попадания выборочных значений в i-й интервал, ${{c}_{i}}~=~({{\alpha}_{i}}_{-\text{1}}+{{\alpha }_{i}})~/2$ – середина i-го интервала, $i=\overline{1,k}$.

При расчёте выборочных характеристик группированной выборки предполагается, что все элементы выборки, попавшие в i-й интервал, находятся в середине интервала. Таким образом, выборочный начальный момент r-го порядка рассчитывается как среднее арифметическое взвешенное середин интервалов, возведённых в r-ю степень, а выборочный центральный момент r-го порядка – как среднее арифметическое взвешенное центрированных середин интервалов, возведённых в r-ю степень. В обоих случаях взвешивание проводится частотами попадания в интервалы:

Пример 3

Выборочной квантилью на уровне вероятности p (или порядка p) выборки x₁,…, x_n называется квантиль случайной величины $X_{n}^{*}$ на уровне вероятности p. Напомним, квантилью случайной величины X называется точная верхняя граница x_p множества значений x, для которых выполнено условие:

$F(x)=P(X<x)=p$.

Для дискретной случайной величины, в частности, для случайной величины $X_{n}^{*}$, точная верхняя граница этого множества не может быть определена однозначно. В связи с этим для расчёта выборочной квантили $x_{p}^{*}$ на практике используются следующие правила.

1. Значение i-го элемента вариационного ряда x_(i) является выборочной квантилью порядка p_i = (i – 0,5) / n. Таким образом, соответствие между элементами вариационного ряда и порядком квантилей устанавливается таблицей

2. Для расчёта квантили произвольного порядка p, 0 ≤ p ≤ 1 используется линейная интерполяция значений, приведённых в таблице выше.

Выборочной медианой выборки x₁,…, x_n называется выборочная квантиль $x_{0,5}^{*}$ на уровне p = 0,5. Из правил расчёта выборочных квантилей следуют правила расчёта выборочной медианы.

1. Если объём выборки n – нечётный, то, разрешая уравнение (i – 0,5) / n = 0,5 относительно i, получаем номер $i=\frac{n+1}{2}$ элемента вариационного ряда, являющегося медианой, т.е.

$x_{0,5}^{*}={{x}_{((n+1)/2)}}$.

2. Если объём выборки n – чётный, то выборочная медиана определяется путём линейной интерполяции элементов вариационного ряда с номерами $\frac{n}{2}$ и $\frac{n}{2}+1$, имеющих порядки квантилей $ 0,5-\frac{1}{n} $ и $ 0,5+\frac{1}{n} $ соответственно. Результатом этой интерполяции будет среднее значение

Выборочные квантили $x_{0,25}^{*}$ и $x_{0,75}^{*}$ на уровнях 0,25 и 0,75 называют выборочными нижней и верней квартилями соответственно. Разность Δ между верней и нижней квартилями называется интерквартильным интервалом:

$\Delta =x_{0,75}^{*}-x_{0,25}^{*}$.

Интерквартильный интервал является характеристикой разброса выборочных значений и является, в некотором смысле, аналогом дисперсии.

Выборочные квантили $x_{0,1}^{*}$,…,$x_{0,9}^{*}$ на уровнях, кратных 0,1, называются выборочными децилями, а выборочные квантили $x_{0,01}^{*}$,…,$x_{0,99}^{*}$ на уровнях, кратных 0,01, – выборочными процентилями.

Выборочной модой выборки x₁,…, x_n с вариантами z₁,…,z_k называется вариант z_i, $i\in \{1,...,k\}$, частота n_i которого максимальна.

Пример 4